![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
注意:これらは学生の研究内容・研究成果であり,教員 (岡本) が各個別テーマに対して専門性を持っているものではありません.
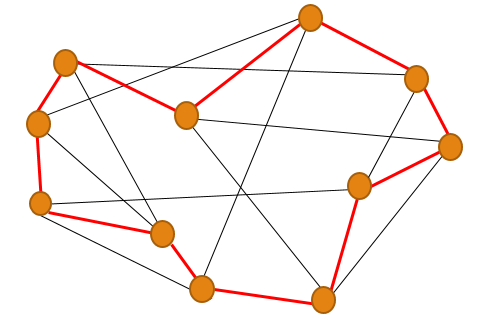
点とそれらを線で結んだものをグラフといい,線をたどってすべての"点"を一度ずつ通ってループを作ることができるかどうかを考えます.このループを我々は「ハミルトン閉路」と呼びます.ハミルトン閉路を含むグラフで,すべての点から出る線の数(次数)が 3であるときには,異なるハミルトン閉路が3つ以上存在するということは1946年に証明 されています(W. T. Tutte).しかし,図のようにすべての点の次数が4であるときにも 同じようなことがいえるかどうかは,45年の間,未解決問題となっています(J. Sheehan, 1975).あらゆる側面から,この問題を証明,あるいは反証することが本研究の目的です.
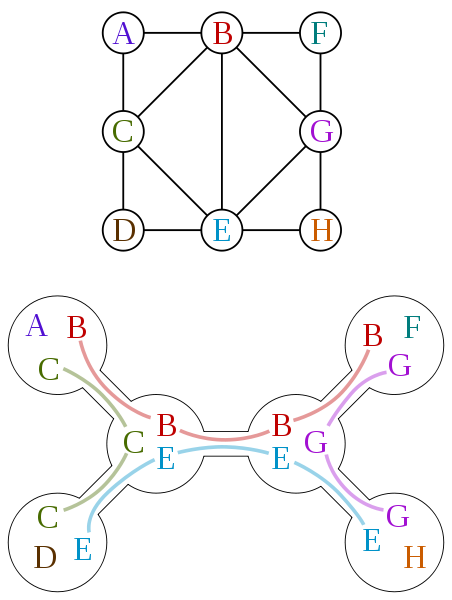
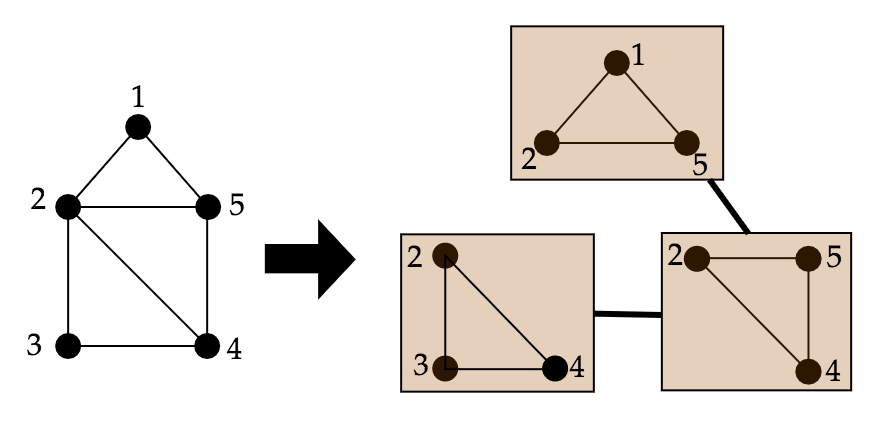
グラフには木分解と呼ばれる概念があります.これはグラフを木の形状(閉路を持たないグラフのこと)になるように,グラフの頂点をある程度まとめて一つの頂点にして,辺を 付け加えることを指します.グラフをうまく木分解するとグラフに関する難しいアルゴリズム(NP完全問題)が簡単に解けることがあり,グラフがうまく木分解で来ているかどうか調べる指標の一つに幅という概念があります.幅はグラフの頂点を一つの頂点にまとめた時の頂点に入っている頂点数から1を引いたものです.(左の下側の図の場合幅は2)幅 はなるべく小さい方が良く,小さい幅をもつ木分解を見つけるアルゴリズムで用いられるPMC(potential maximal clique)と呼ばれる概念について研究しています. (図の出典は https://ja.wikipedia.org/wiki/木分解 です. )
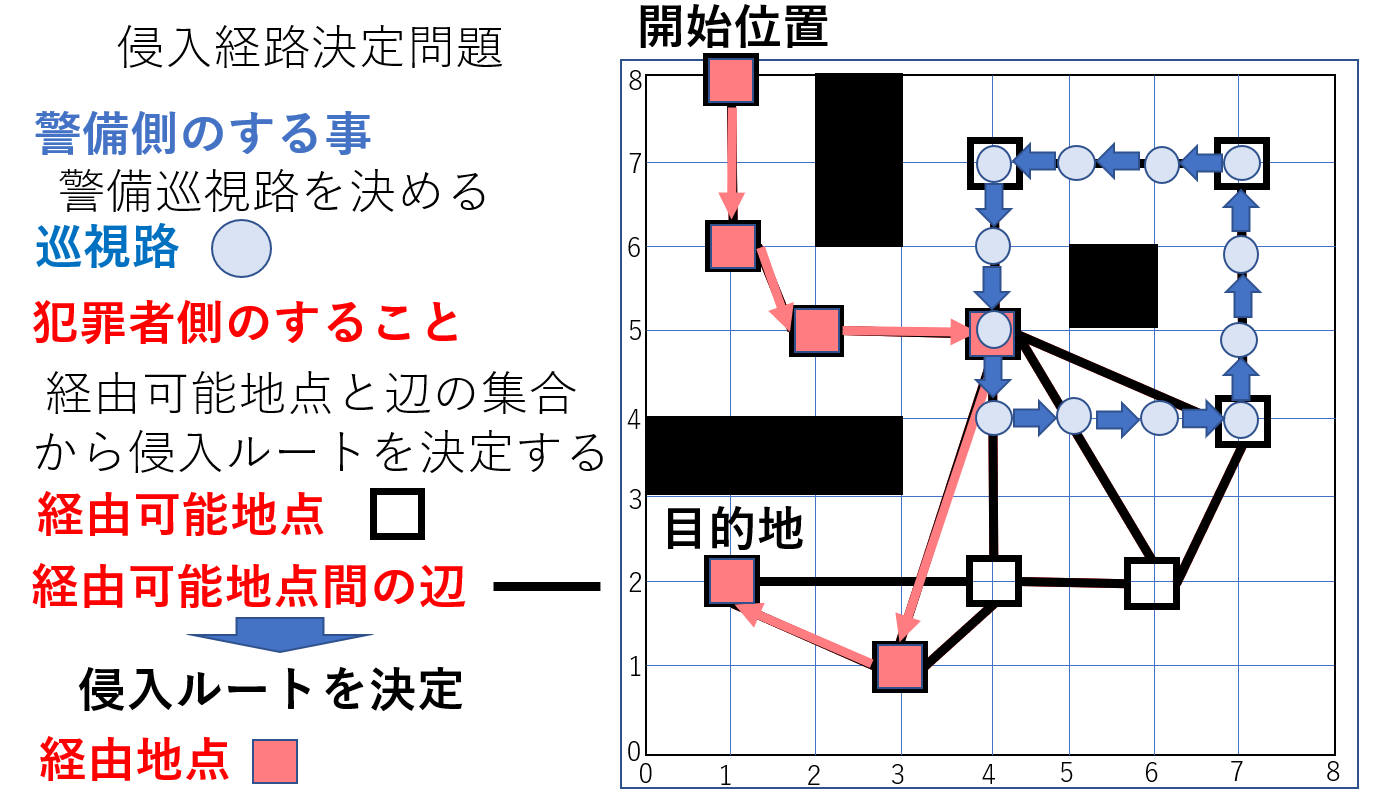
近年, 人件費の増大やセンサー技術の進歩により, 効率の良い警備人員や監視カメラ等の配置を行うアルゴリズムが注目されている. ある対象への効率的な警備資源の分配を考える問題を「警備理論」と言い, ある施設への効率的な警備配置を考える問題を「施設警備ゲーム」と言う. 私の行っている研究では, 二次元平面上に設定した施設への効率的な 警備員や警備機械の配置を考える問題のモデル化と, その問題を効率的に解く離散アルゴリズムの考案および実験です. 可能なすべての警備員, 機械の配置を考えると膨大な計算時間がかかってしまう問題でも, 数理計画法と呼ばれる最適化アルゴリズムを用いる事で 効率良く最適解を求めることが出来ます. 図に示した「侵入経路決定問題」では, 二次元平面上での侵入者の侵入方法を考える事で, 警備員の警備配置を評価する問題です.

離散ホタルアルゴリズムは,オスのホタルが強い光を放っているメスへ飛んでいく求愛行動をモデル化したアルゴリズムです.問題の最適解を計算で求めるのが難しい問題に対して有効で,例を挙げると効率的な生産スケジュールや配送ルートを求める際に用いられます.各ホタルが問題に対する解を持っているとし,評価の高い解を持っているホタルへ解を少しずつ近づけることで最良解を発見します.同種のアルゴリズムと比較すると,解を発見するまでの過程が簡単であることや本実験を行うまでの準備が短いことが特徴です.研究の目的は離散ホタルアルゴリズムの改良を行い,以前のアルゴリズムや同種のアルゴリズムと比較します.
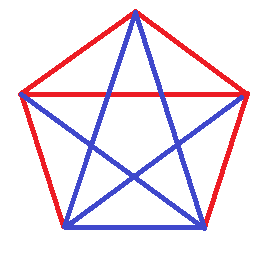
n個の点が存在し,そのどの2点も線で結ばれているようなものを考えます.図は,nが5の場合です.ここで,線を適当に赤と青で塗り分けることを考えます.このとき,同じ色だけを使い,同じ線を二度以上使わないような経路(小道といいます)を考えてみましょう.図の場合では,赤い線を4本使った経路と,青い線を4本使った経路があります.研究では,線をどのように赤と青で塗り分けたとしても,どちらかの色だけを用いて長さがkの小道が出来てしまうようなnの範囲について考察しています.
最短経路を求める問題や、地図の色を塗り分けるのに必要な色の数を求める問題、といったいくつかの問題はグラフを用いて問題を定式化できます。このような問題にはしかし、効率的に解を求めることができる解きやすい問題が存在する一方で、実際に解くには計算時間がかかる難しい問題が多く存在します。そのような難しい問題を効率的に解くための方法の一つとして、解きやすい問題の構造に似ている度合いを表す指標(パラメーター)を用いて、似ている構造をもつ場合には速く解けるような方法があります。そのような問題の構造を表す指標は、これまでにいくつか提示されていますが、より複雑なグラフを表すことができるような指標の表現方法に興味を持っています。

こいこいは、安土・桃山時代の天正かるたに由来すると言われるカード「花札」を使ったゲームです。二人のプレイヤーが順番にカードを取っていき、特定の組が完成した時点で得点を得ることができます。また麻雀のように上がれる状況でも、あがらない「こいこい」を選択できるのが特徴です。私はある時点においてどちらかのプレイヤーが必勝であるか、またはその計算が複雑であるかについて証明しようと考えています。必勝であるとは、相手がどのような行動をとったとしても勝つことができる行動が存在することを言います。

ゲーム理論とは、人間、会社、コンピュータなどの複数の主体がそれぞれ意思決定をして、自身の利益を大きくしようとする様子を取り扱う分野です。特に、プレイヤ同士が合意のもとで協力関係を結べる状況を協力ゲームといいます。この協力関係を提携と呼び、協力ゲームでは提携ごとに得られる利益が与えられます。
昔から研究されているような協力ゲームでは、1人のプレイヤは2つ以上の提携に参加出来ないものとしています。しかし現実には、1人の人間が2つ以上のチームに参加して仕事をするような場合など、プレイヤが複数の提携に参加するような場合も存在します。提携を構成するプレイヤに重複があるような協力ゲームにおいて、どのように提携を組むと利益が大きくなるのか、得られた利益はどのように分配するのが良いのかという問題の研究をしています。

無向グラフは,いくつかの頂点と,いくつかの辺からなります.1つの辺は異なる2つの頂点を結び,辺の向きはありません.この研究では,「ある1つの色で塗られた頂点からなる閉路が存在しない」という制限を課して各頂点に色を塗ることを考えます.ここで閉路とは,ある頂点から辺でつながれている頂点を1個以上経由して元の頂点に戻ってくるような経路のことです.このような塗り方を頂点樹化彩色といい,その色の数の最小値,もしくは色の数が最小となるような塗り方を求める問題を頂点樹化彩色問題といいます.例えば,図の塗り方は頂点樹化彩色になっています.このグラフには閉路が複数含まれていますが,同一の色のみで塗られた閉路は1つも存在しません.頂点樹化彩色問題はNP困難(つまり,難しい)ということが知られています.この研究では,特別な頂点樹化彩色問題に関して成り立つ定理などを発見しようとしています.