学生の研究 (2022年度版)

学生の研究 (2022年度版)†

注意：これらは学生の研究内容・研究成果であり，教員 (岡本) が各個別テーマに対して専門性を持っているものではありません．

現在のメンバーの研究†

辺追加による影響最大化†

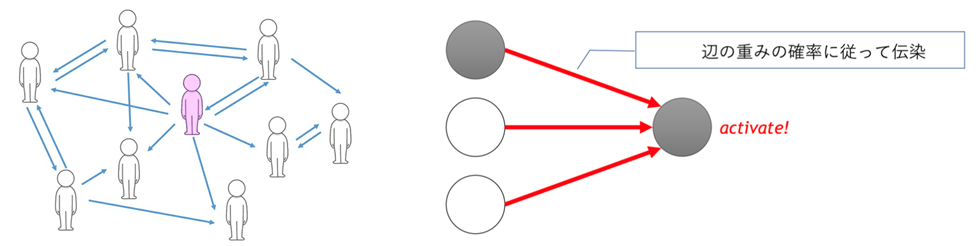
バイラルマーケティングとは，SNSや口コミを利用して不特定多数の人に情報を拡散する手法です．これを効率的に行うために，SNSをグラフでモデル化し，より多くの人に情報を届ける手法の研究が盛んに行われています．グラフの頂点にあたる"情報の発信源"に着目した研究が既に多く存在しますが，私の研究ではグラフの辺にあたる，ユーザー同士のフォローといった"関係性"に着目し，情報拡散を促すアルゴリズムの開発を目指します．

↑

ボロノイ図とディグフォーメーション†

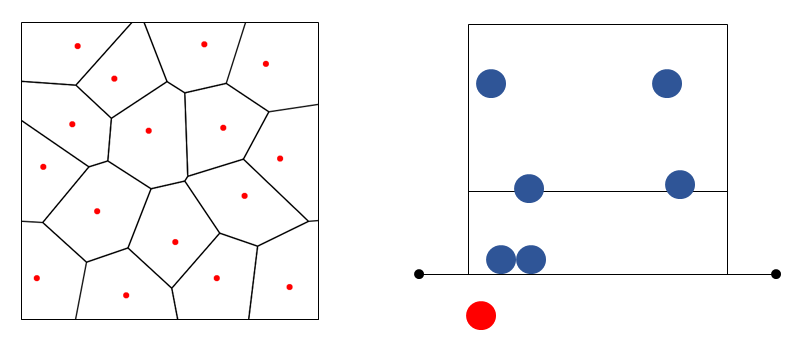
ボロノイ図とは，与えられたいくつかの点に対し，どの点に一番近いかによって領域を分けた図です．一方，バレーボールにおいて，スパイクをレシーブすることをディグと呼び，その際のフォーメーションをどのように設定するかは重要な戦略の一つとなっています．ディグフォーメーションをボロノイ図で表現することで，フォーメーションの数学的な分析を行うことを目指します．

↑

マッチングKneserグラフのハミルトン閉路†

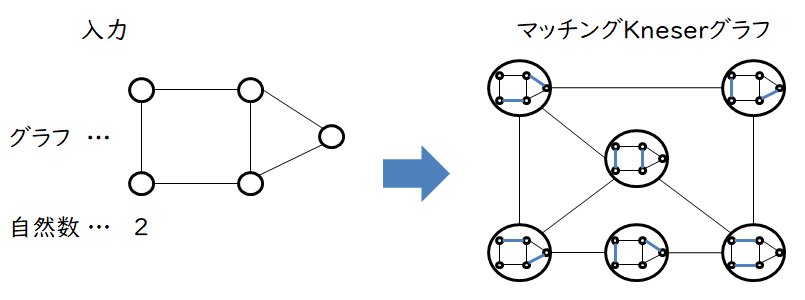
グラフ理論において，ある頂点から，すべての頂点を一度だけ通って元の頂点に戻ってくる道のことをハミルトン閉路といいます．与えられたグラフがハミルトン閉路をもつかどうかを判定することは難しい問題として知られています．私の研究では，入力としてグラフと自然数が1つずつ必要なマッチングKneserグラフというグラフについて，どのような入力であればマッチングKneserグラフはハミルトン閉路をもつのかを調べています．

↑

“小さい”グラフマイナーの研究†

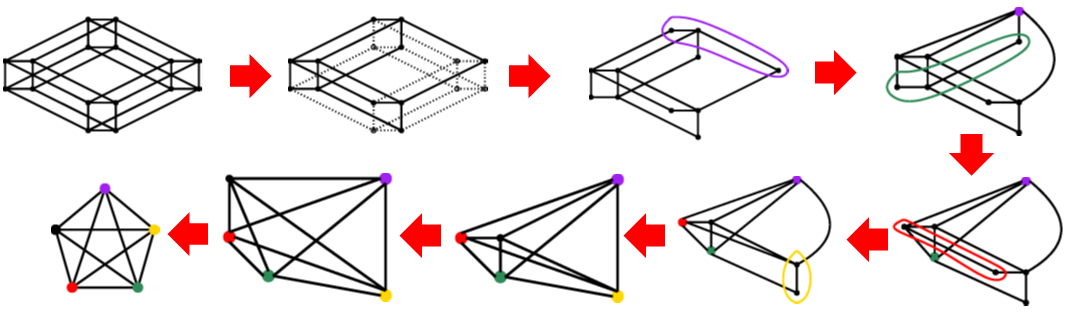
「元のグラフ」から，頂点や辺を削除したり，いくつかの隣り合った頂点を一つの頂点とみなしたりして，「別のグラフ」を得ることを考えます．このとき，「別のグラフ」は「元のグラフ」の「マイナー」であると言います．研究では，「元のグラフ」と「マイナー」が与えられたとき，「マイナー」を得るために必要な「元のグラフ」の最小の部分はどこか，与えられたグラフの性質からその部分が最小であることが示せるのか，といったことを明らかにすることを目標にしています．

↑

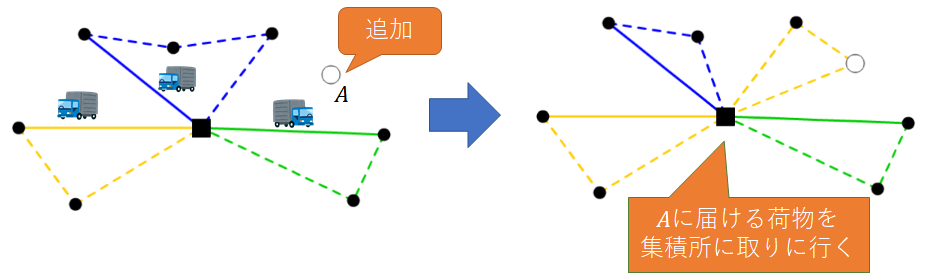
注文した日に配達を完了させるには†

配送中であるにも関わらず次々に配送先が増えていくとき，最適な配送経路を探索することを目指します．既存の研究では車両が配送先を訪問すればよいとされていたところを，この研究では各荷物が確かに配送先に届けられることまで想定します．この問題を配送計画問題という配送に関する最適化問題をもちいてモデル化し，それを解くための効率的なアルゴリズムを研究しています．

↑

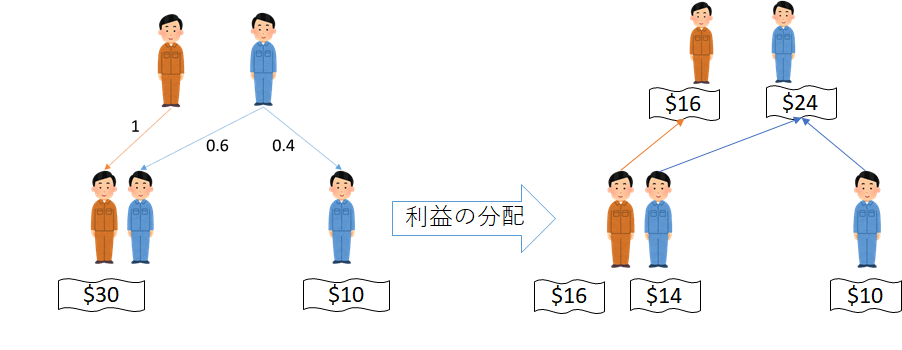
仲裁コアの非空性†

Overlapping Coalition Formation ゲーム(OCFゲーム)は、協力ゲームの拡張であり、複数の主体がリソースを分割して協力できる場合をモデル化しています．協力関係による利益は参加者で分配され、誰からも不満が出ないような協力関係と分配の仕方のペアの集合を仲裁コアといいます．この仲裁コアが空集合ではなくなるのはどんなときかについて研究しています．

↑

マインスイーパーの難易度†

マインスイーパーは,数百個のマス目からなる地雷原から地雷のあるマスを特定し，地雷が埋まっていないマスを全て開けるゲームです．地雷の埋まっていないマスを開けると，その周囲の8マスにある地雷の数を示す数字が表れます．この情報を用いて，どのマスに地雷が埋まっているかを推測します．私の研究では,マインスイーパーの難易度に関する新しい指標を考案することを目標とします．

↑

ヴァイオリンの運指最適化†

4弦からなる弦楽器の一種であるヴァイオリンには1つの音高に対して複数の押弦パターンが存在します．また楽譜に指示がないとき，奏者は押弦パターンを自ら選択する必要があります．私の研究では押弦に用いる4本の指の運動量に着目し，楽譜の情報から奏者にとって負担の少ない運指を導出することを目標としています．

↑

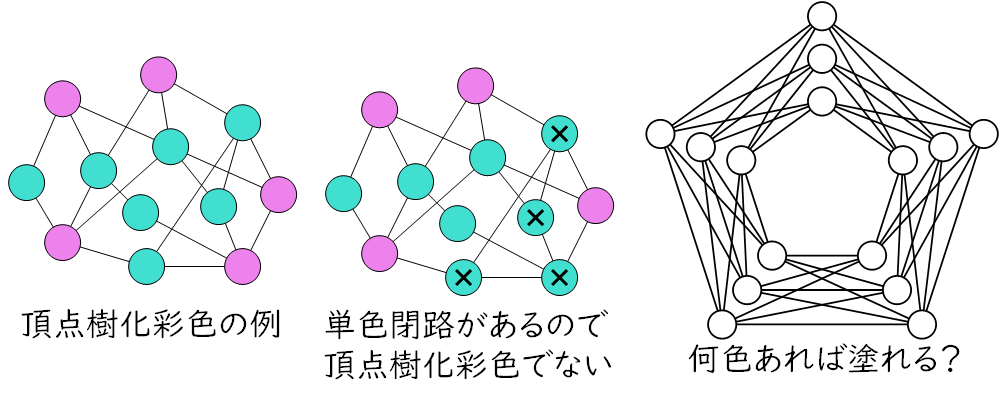
無三角グラフの頂点樹化彩色†

グラフの頂点に色を塗ることを考えます．ただし，単色閉路があってはいけません．このような塗り方に必要な最小の色数を求める問題を頂点樹化彩色問題といいます．一般のグラフに対して頂点樹化彩色問題は難しいことが知られています．本研究では，無三角グラフというグラフに対して頂点樹化彩色問題を解くことを目指します．

↑

過去の卒業論文，修士論文†

↑

令和3年度†

対数空間による非切断辺数の推定と木判定 (修士論文)
道分解における潜在極大クリークの研究 (修士論文)
クリーク幅の構成表現に対するグラフ分解手法の適用の検討 (修士論文)
部分当日配送計画問題の提案とLin-Kernighan-Helsgaun法を用いたアルゴリズムの実装 (卒業論文)
頂点数9の完全グラフの非反復辺染色数の特定 (卒業論文)
グラフ上のSolitaire Clobber Gameとcorreducibilityに対する連結度からの考察 (卒業論文)

↑

令和2年度†

カバー関数を用いた施設警備ゲームのモデル化 (修士論文)
4正則一意的ハミルトニアングラフの存在性 (修士論文)
フレキシブルジョブショップスケジューリング問題に対する離散ホタルアルゴリズム (修士論文)
花札のこいこいにおける必勝戦略計算可能性 (卒業論文)
頂点数12以下の無三角グラフの頂点樹化数 (卒業論文)
提携に重複を許したロバストな提携構造形成問題の研究 (卒業論文)

↑

令和元年度†

Rook-Fáry Drawingの存在性 (修士論文)
小道に関するラムゼー数 (卒業論文)
ペンシルパズル「ぬりみさき」の物理的ゼロ知識証明 (卒業論文)

↑

平成30年度†

Cops and Robbers gameの研究 (修士論文)
時間枠付き輸送経路問題に対するハイブリッドアントコロニー最適化法の提案 (修士論文)
位置情報ゲームIngressにおける制限時間内で得られる経験値の最大化近似アルゴリズム (修士論文)
多重リスト彩色に対する保証付きアルゴリズム (修士論文)
排他制約付き厳密被覆問題に対するZDDを用いた解列挙手法 (修士論文)
数理計画法を用いた施設警備ゲームに関する研究 (卒業論文)
始点固定ハミルトンパスの唯一存在性に関する研究 (卒業論文)
変形可能な物体の2次元パッキング問題 (卒業論文)

↑

平成29年度†

限定記憶を持つプレイヤーのための戦略設計 (修士論文)
グラフのフィードバック頂点集合問題に対する局所探索法 (修士論文)
疎性をもつ半正定値計画問題の変換手法における弦拡張に関する研究 (卒業論文)
rook-straight line drawing が存在するグラフクラスに関する研究 (卒業論文)
Pyramidの計算複雑性 (卒業論文)

↑

平成28年度†

ランダムグラフ上の最長路問題に対する発見的アルゴリズム (修士論文)
快適さを最大化する公園の散歩経路設計 (卒業論文)
位置情報ゲームIngressにおける制限時間内で得られる経験値の最大化 (卒業論文)
弱双対が線型森である外平面的グラフのゲーム染色数 (卒業論文)
橋をかけろの解答・問題生成アルゴリズム (卒業論文)

↑

平成27年度†

一次元版クロバーの解析 (修士論文)
単位円グラフのセパレータ構成問題に対するアルゴリズム的研究 (修士論文)
A Comparison with an Approximation Algorithm for the Geometric Firefighter Problem (卒業論文)
N面サイコロを用いたLiar's DiceおよびBluffにおける最適戦略の導出アルゴリズム (卒業論文)
位相幾何学的データ解析を用いたPOSデータの分類 (卒業論文)
重み付き木における探索戦略決定問題の研究 (卒業論文)
逆算法によるラッシュアワーの盤面の列挙 (卒業論文)

↑

平成26年度†

音楽シミュレーションゲーム「jubeat」に対する運指最適化 (卒業論文)
確率的に構成したグラフにおける最長路問題の性質 (卒業論文)
カードゲーム「チェント」における戦略の解析 (卒業論文)

↑

平成25年度†

逐次添加サンプリング方式によるパラメータ自動チューニングに関する研究 (修士論文)
マルチGPU環境におけるCRS形式疎行列・ベクトル積の入力行列の最適化による高速化 (修士論文)
村田法のスレッド並列化によるマルチコアCPU上での実対称帯行列帯幅縮小操作の高速化 (修士論文)
自転車詰込み問題 (卒業論文)
視聴率とTwitter検索のヒット数に関するデータ分析 (卒業論文)
スコットランドヤードに対する思考ルーチンの作成 (卒業論文)
セル・オートマトンモデルによるエスカレータ通行のモデル化 (卒業論文)
トレーディングカードゲームにおける初手確保基準のモデル (卒業論文)
Magnus-Derek gameにおける最小の手数 (卒業論文)

(文責：岡本吉央)

メニュー

↑

学生の研究 (2022年度版)