学生の研究†
注意:これらは学生の研究内容・研究成果であり,教員 (岡本) が各個別テーマに対して専門性を持っているものではありません.
現在のメンバーの研究†
指定する頂点同士を結ぶ道を見つけるには?†
頂点と頂点同士を辺で結んでできる構造をグラフといいます.
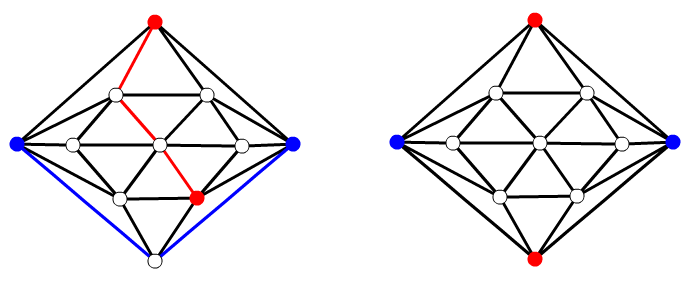
本研究では,いくつかの頂点の組が指定されて,その指定された頂点同士を結ぶ交わらない道が見つかるかという問題を考えています.
例えば,図にある2つのグラフで同色の頂点同士を結ぶ交わらない道が見つかるかを考えます.実は,左のグラフは見つけられますが,右のグラフには見つかりません.
このように,同じグラフでも指定する頂点によっては道が見つかったり見つからなかったりします.
本研究では,どんな性質をグラフが満たしていれば,どのように頂点の組を指定しても互いに交わらない道が見つかるのかや,
指定する頂点の組を増やしたらどうなるのかといったことを研究しています.
複数の文の圧縮についての研究†
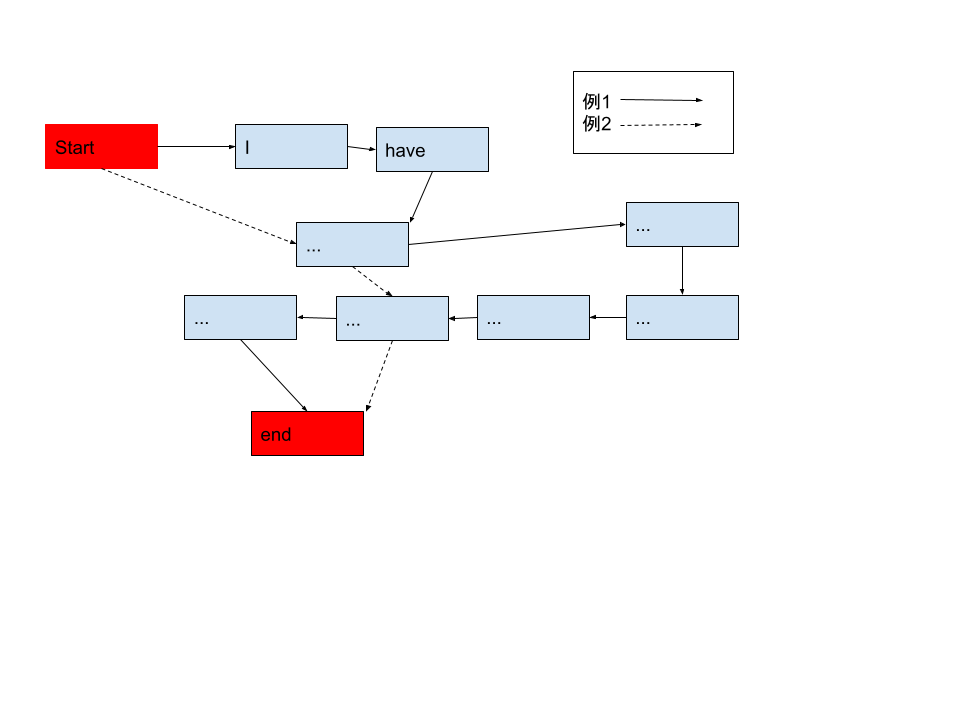
ウィキペディアなどのウェブサイトでは、様々な問題に関する情報が提供されています。しかし、それらの文章は長く、情報は多すぎるので自動テキスト要約(ATS)できるアプリがあると便利です。この時、文法的に正しく、形の整った小さな文を生成するためにMSC を用いることがあります。Multi-Sentence Compression (MSC)とは密接に関連する複数の文から新たに文章を生成することです。これはATSよりも情報量の多い要約を生成することがあります。このときにできるだけ情報が落ちないようにすることとできるだけ短い文を生成することが重要です。主要な手法として次のようなものがあります。ラベル付きグラフを用いてK最短経路を生成します。そして、整数線形計画法を用いて生成された最短経路の集合から文を選択します。興味があるのはこの手法を分析してより優れた要約の手法を編み出すことについてです。
グラフの特徴を表すような指標を求めるアルゴリズムの検討†
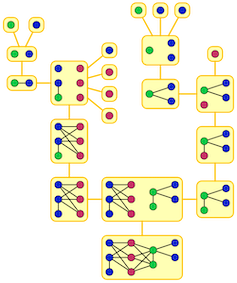
最短経路を求める問題や地図の色を塗り分けるのに必要な色の数を求める問題、といったいくつかの問題は、”グラフ”という頂点と辺からなる問題の表現方法を用いて問題を定式化できます。このような問題にはしかし、効率的に解を求めることができる解きやすい問題が存在する一方で、実際に解くには計算時間がかかる難しい問題が多く存在します。そのような難しい問題を効率的に解くための方法の一つとして、解きやすい問題の入力の構造に似ている度合いを表すようなグラフの指標を用いて、その指標の値が小さい場合には速く解けるような方法があります。しかし、あるグラフが与えられたときにそのグラフの指標の値を求めること自体に計算時間がかかってしまうという問題があります。そこで研究では、グラフの指標を早く計算する方法を考察しています。(図の出典: https://en.wikipedia.org/wiki/Clique-width )
SNSにおける影響最大化問題†
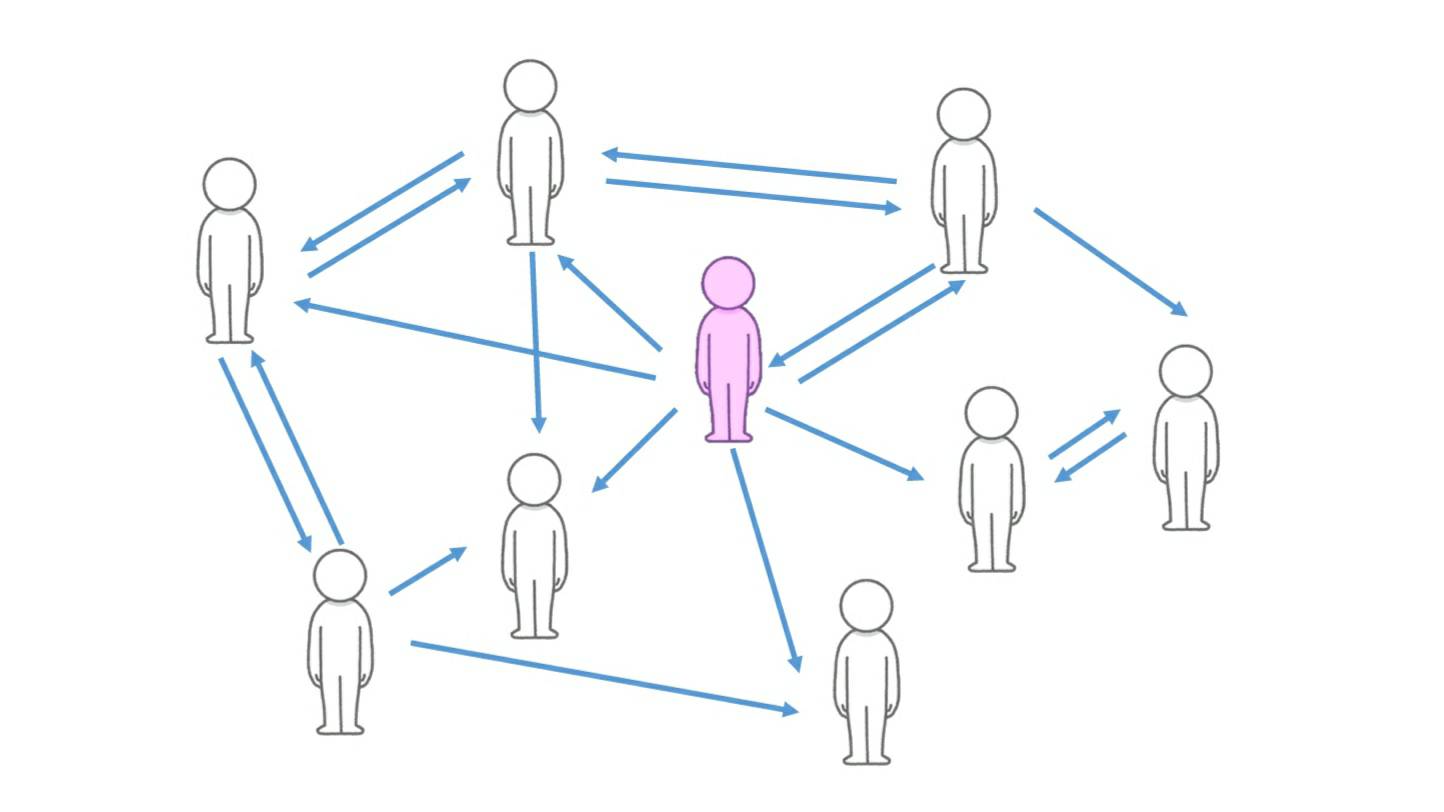
商品の宣伝や災害情報の周知など,情報の拡散は社会の重要な要素の一つとなっています.そこで,特に情報の収集及び発信が手軽なSNSをモデルにし,発信した情報をより多くのユーザーに届けるように促す手法について研究しています.
研究のテーマである影響最大化問題とは,グラフにおける最適化問題の一つであり,既に多くの研究があります.SNSのモデルにおける影響最大化問題とは,情報の発信源であるユーザーの数を入力として予め定め,その条件の下で最も多くのユーザーに情報を拡散することのできる発信源ユーザーの集合を出力する問題です.本研究では,このような情報源ユーザーの集合の選択以外の手法による影響最大化問題について,問題設定とそれを解くアルゴリズムの提案を目的としています.
配送計画問題の研究†
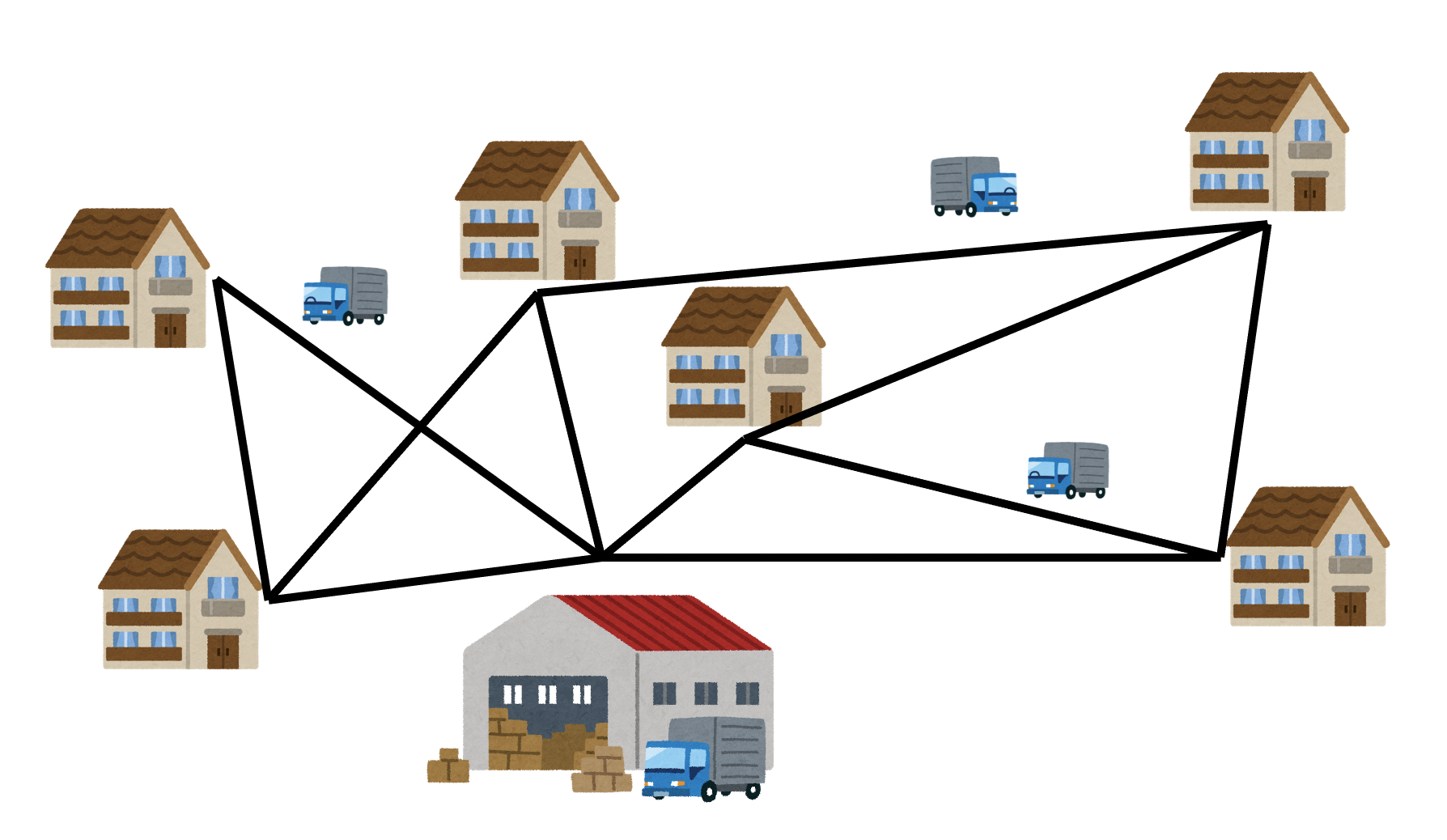
数学においてグラフとは頂点と辺からなるものを指します。現実の事象をグラフとして単純化することで、様々な問題を解くことが可能です。配送計画問題は場所を頂点、道を辺としてグラフに落とし込むことで、最適な輸送経路を見つけることを目的とします。配送計画問題の内容は多岐に渡りますが、その一例として配達が挙げられます(図参照)。1つの頂点を物流センター、他の頂点を顧客とみなし、物流センターから各顧客(あるいはその逆)への配送を複数のトラックで行う時、各トラックの最適な経路を求めます。そのような経路を求めるアルゴリズムはどのようなものか、そのアルゴリズムはどれほど有用かを調べることが本研究の目的です。
過去の卒業論文,修士論文†
令和2年度†
- カバー関数を用いた施設警備ゲームのモデル化 (修士論文)
- 4正則一意的ハミルトニアングラフの存在性 (修士論文)
- フレキシブルジョブショップスケジューリング問題に対する離散ホタルアルゴリズム (修士論文)
- 花札のこいこいにおける必勝戦略計算可能性 (卒業論文)
- 頂点数12以下の無三角グラフの頂点樹化数 (卒業論文)
- 提携に重複を許したロバストな提携構造形成問題の研究 (卒業論文)
令和元年度†
- Rook-Fáry Drawingの存在性 (修士論文)
- 小道に関するラムゼー数 (卒業論文)
- ペンシルパズル「ぬりみさき」の物理的ゼロ知識証明 (卒業論文)
平成30年度†
- Cops and Robbers gameの研究 (修士論文)
- 時間枠付き輸送経路問題に対するハイブリッドアントコロニー最適化法の提案 (修士論文)
- 位置情報ゲームIngressにおける制限時間内で得られる経験値の最大化近似アルゴリズム (修士論文)
- 多重リスト彩色に対する保証付きアルゴリズム (修士論文)
- 排他制約付き厳密被覆問題に対するZDDを用いた解列挙手法 (修士論文)
- 数理計画法を用いた施設警備ゲームに関する研究 (卒業論文)
- 始点固定ハミルトンパスの唯一存在性に関する研究 (卒業論文)
- 変形可能な物体の2次元パッキング問題 (卒業論文)
平成29年度†
- 限定記憶を持つプレイヤーのための戦略設計 (修士論文)
- グラフのフィードバック頂点集合問題に対する局所探索法 (修士論文)
- 疎性をもつ半正定値計画問題の変換手法における弦拡張に関する研究 (卒業論文)
- rook-straight line drawing が存在するグラフクラスに関する研究 (卒業論文)
- Pyramidの計算複雑性 (卒業論文)
平成28年度†
- ランダムグラフ上の最長路問題に対する発見的アルゴリズム (修士論文)
- 快適さを最大化する公園の散歩経路設計 (卒業論文)
- 位置情報ゲームIngressにおける制限時間内で得られる経験値の最大化 (卒業論文)
- 弱双対が線型森である外平面的グラフのゲーム染色数 (卒業論文)
- 橋をかけろの解答・問題生成アルゴリズム (卒業論文)
平成27年度†
- 一次元版クロバーの解析 (修士論文)
- 単位円グラフのセパレータ構成問題に対するアルゴリズム的研究 (修士論文)
- A Comparison with an Approximation Algorithm for the Geometric Firefighter Problem (卒業論文)
- N面サイコロを用いたLiar's DiceおよびBluffにおける最適戦略の導出アルゴリズム (卒業論文)
- 位相幾何学的データ解析を用いたPOSデータの分類 (卒業論文)
- 重み付き木における探索戦略決定問題の研究 (卒業論文)
- 逆算法によるラッシュアワーの盤面の列挙 (卒業論文)
平成26年度†
- 音楽シミュレーションゲーム「jubeat」に対する運指最適化 (卒業論文)
- 確率的に構成したグラフにおける最長路問題の性質 (卒業論文)
- カードゲーム「チェント」における戦略の解析 (卒業論文)
平成25年度†
- 逐次添加サンプリング方式によるパラメータ自動チューニングに関する研究 (修士論文)
- マルチGPU環境におけるCRS形式疎行列・ベクトル積の入力行列の最適化による高速化 (修士論文)
- 村田法のスレッド並列化によるマルチコアCPU上での実対称帯行列帯幅縮小操作の高速化 (修士論文)
- 自転車詰込み問題 (卒業論文)
- 視聴率とTwitter検索のヒット数に関するデータ分析 (卒業論文)
- スコットランドヤードに対する思考ルーチンの作成 (卒業論文)
- セル・オートマトンモデルによるエスカレータ通行のモデル化 (卒業論文)
- トレーディングカードゲームにおける初手確保基準のモデル (卒業論文)
- Magnus-Derek gameにおける最小の手数 (卒業論文)
(文責:岡本吉央)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)